

Автор приводит альтернативную существующим методику расчёта П-образного контура с примерами практических расчётов. Статья размещается в качестве полемической. Желающие участвовать в её обсуждении могут воспользоваться электронным адресом автора, размещённым в статье, либо зайдя в раздел "КВ техника" на форуме владимирских радиолюбителей.
П-контур широко применяется радиолюбителями как с целью частотной фильтрации, так и трансформации сопротивлений в выходных и межкаскадных цепях усилителей. Аналитический метод расчёта П-контура (П-к) для широкого круга радиолюбителей был предложен в [1]. Долгое время он использовался для расчёта ламповых усилителей мощности, в которых эквивалентное сопротивление Rэ источника много больше сопротивления нагрузки Rн. Но, в решении системы нелинейных уравнений были допущены упрощения, и, в общем случае, точность расчётов оставляла желать лучшего. Эта работа послужила основой для уточнённого метода расчёта П-к [2], который можно применять как для выходных согласующих (фильтрующих) устройств усилителей мощности, так и для межкаскадных связей в ламповых и транзисторных схемах.
Однако из-за слабой информационной связи между радиолюбителями - конструкторами в литературе появляется информация настоятельно рекомендующая устаревшую методику [1], например в [ 3]. Поэтому постараюсь по-возможности кратко изложить основы методики [2].
 |
 |
|---|
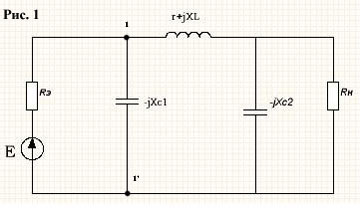
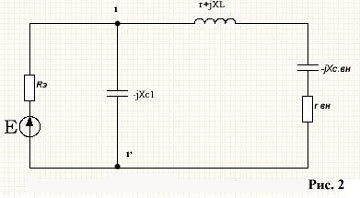
Принципиальная схема П-к на рис.1 может быть упрощена заменой параллельного соединения конденсатора C2 и резистора Rн на эквивалентное последовательное соединение зависимых от частоты внесенных сопротивлений rвн и xс.вн:
Rн × XC22
rвн = ----------- ; (1)
Rн2 + XC22
Rн2 × XC2
Xc.вн = ----------- ; (2)
Rн2 + XC22
Согласно рис.2 положим, что эквивалентное индуктивное сопротивление второй ветви (рис.2) XLЭ = XL - xc.вн; r = rL + rвн. Тогда комплексная входная проводимость в точках 1 и 1':
1 1 1 1 r - jXLЭ
---- = ----- + --------- = j ----- + ---------- .
Zвх -jXC2 r + jXLЭ XC2 r2 + XLЭ2
В последнем выражении мы избавились от мнимости в знаменателе. Запишем его в виде:
1 r 1 XLЭ
---- = --------- + j (---- - ---------) . (3)
Zвх r2 + XLЭ2 XC2 r2 + XLЭ2
На резонансной частоте (ω = ωр) входная проводимость чисто активна и равна проводимости источника 1 ⁄ Rэ, а мнимая часть = 0:
1 r
--- = ----------- (4)
Rэ r2 + XLЭ.р2
а из (3):
r2 + XLЭ.р2 = XLЭ.р × XC1.р . (5)
Следовательно,
1 r 1
---- = ------------ = ----------,
Rэ XLЭ.р × XC1.р Qн × XC1.р
где нагруженная добротность контура на резонансной частоте
XLЭ.р Qн = ----- r
Тогда,
RЭ XC1.р = ----- . (6) Q н
Так как
1 Q н
----- = ωрС1 = ----,
XC1.р RЭ
то становится понятным, что одной из причин падения выходной мощности лампового усилителя в верхней части любительского диапазона может быть повышенное значение требуемой Qн при данной минимально возможной емкости С1, что приводит к увеличенным потерям в П-к и снижает КПД. Ситуация улучшается при уменьшении RЭ.
Значение XLЭ.р = r Q н подставим в (4) и находим:
RЭ
r = ---------. (7)
QH2 + 1
Заметим, что КПД П-к η = rвн ⁄ r , а из (1):
Rн XC22 rвн = ηr = ----------. Rн2 + XC22
Следовательно,
Rн
XC2p = ------------------ (8)
Rн
√(----- - 1)
(ηr)
На основании вышеизложенного: XL = XLЭ + Xс.вн; XLЭ = r QH;
Rн Xс.вн = rвн ---- см. уравнения (1) и (2). XC2
Поэтому,
Rн XL = rQH + rвн ----. XC2
Так как rвн = η r, то
Rн XLp = r(QH + η -----). (9) XC2p
Формулы (6), (7), (8), (9) позволяют найти значения величин элементов П-к с потерями для данной резонансной частоты. Полоса пропускания такого несимметричного по нагрузке фильтра увеличивается с уменьшением QH. Для симметричных фильтров, без учёта потерь, минимум коэффициента передачи напряжения в области пропускания находится на относительной частоте Ymin = 1 ÷ √ 3. Формулы данной методики точны и много проще формул по методике [1].
Продолжим обсуждение вопроса. При симметричной нагрузке (RЭ = Rн) в режиме согласования П-к должен быть симметричным, что следует из (6) и (8). При отсутствии потерь в П-к выходные напряжения в начале АЧХ и на частоте резонанса, естественно, совпадают, а в полосе пропускания появляется некоторый «завал» в виде седловины, увеличивающийся с увеличением Qн. Можно показать, что независимо от Qн, минимум седловины находится на относительной частоте ωmin ⁄ ωP = Ymin. В таблице показана зависимость нормированного коэффициента передачи напряжения Kmin(Ymin), как функции QH (вторая строка таблицы).
| 0,99464 | 0,98198 | 0,96479 | 0,94184 | 0,91435 | 0,88378 | 0,85148 | 0,81854 | 0,79966 | 0,73049 |
|---|---|---|---|---|---|---|---|---|---|
| 0,75 | 1 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,5 | 2,75 |
При выборе промежуточных точек достаточна линейная интерполяция. Как показано в (2), минимум седловины не зависит от R. Из таблицы видно,что фильтр нижних частот с приемлемой равномерностью имеет низкую добротность нагруженного контура и, только в этом случае, может применяться в широкополосных фильтрах.
Строго говоря, расчёт таблицы проведен для η = 1. Из (6), (7), и (8) следует, что ХC1 не равняется XC2, и максимум неравенства увеличивается с уменьшением QH. Расчёт для η = 0.95 и QH = 1 (меньшее значение применять не следует) - погрешность не превышает 5 %, что вполне допустимо при радиотехнических расчётах.
Если QH > 5, то фильтр образует узкополосную систему с глубоким провалом седловины, с лучшей фильтрацией высших гармоник и ухудшенной фильтрацией низких частот вне рабочего диапазона и субгармоник. Следует заметить, что методика расчёта [1], в отличие от предлагаемой, не работает при симметричной нагрузке. Проверка для QH = 2, R=50 Ом, η = 0.95 по методике [1] показывает, что:
50 - 0,95 × 50
XC2 = -------------------------------- = 4,378997 Ом;
1
√----- × (5 - 0,952) - 2 - 0,95
0,95
50
XC1 = ---------------------- = - 5,651148 Ом.
(2 × XC2 - 0,95 × 50)
По методике [2], XC1 = 50 ÷ 2 = 25 Ом. Правильные методики не могут дать разных результатов. Но методика [2] обоснована в настоящем материале, в то время, как автор [1] в своей работе указывал на приближённость его метода расчёта, основанного на предположении, что КПД П-к
QH
η = 1 - -----,
QXX
где QXX - нагруженная добротность в режиме холостого хода. В следующей части статьи будет показано, что данная формула стала расхожим мнением о её правильности благодаря некорректному её выводу в учебнике по радиотехнике для высших учебных заведений, и приведём примеры расчёта П-к для широкополосных и узкополосных фильтрующих систем.
При симметричной нагрузке Rн = Rэ фильтр в виде П-к не симметричен (Xc1 ≠ Xc2):
RЭ2 RН2 = RЭ2
Xc1p2 = ----, Xc2p2 = ---------- ,
QН2 QН2 1
---- + ---
η η
равенство возможно только в случае η = 1. Отличие в этих выражениях находим их делением (η = 0.95), при Qн = 1 → 1.1052, Qн = 3 → 1.0584.
Для широкополосных ФНЧ погрешность вполне допустима при радиотехнических расчётах, используя таблицу. При симметричном П-к (Xc1р = Xc2р) нагрузка, как мы видели, будет симметричной только в случае η = 1.
В общем случае из равенства Xc1p2 = Xc2p2 находим (применим (6), (7), (8)):
RH RH 1 RH
QH2 × ---- ( ---- - --- ) = ------ - 1.
RЭ RЭ η η × RЭ
При η = 1:
QH2 × RH RH
(--------- - 1) × (--- - 1) = 0
RЭ RЭ
В последнем случае симметричный П-к может работать на согласованную нагрузку не только при Rн = Rэ, но и при Rэ ÷ Rн = Qн2; тогда Xc1р = Xc2р = XLр. Такой П-к обычно называют антиметричным. В общем случае (η ≠ 1) коэффициент трансформации Rн ÷ Rэ находится из предыдущего равенства.
Таким образом, симметричные фильтрующие системы с П-к, строго говоря, не существуют. Однако применение расчётных формул в предположении η = 1 с приемлемой для практики точностью более удобны. Кроме тех случаев, когда требуется определить потери в самом П-к, которые при малых добротностях достаточно малы.
Важный вопрос, когда можно пренебречь величиной
rвн
η = --------- ?
rL + rвн
Когда rL << rвн.
Расчёт показал, что для η ≥ 0.95, необходимо иметь rвн ≥ 20 rL. Определение величины rL теоретическим расчётом сложно, и для каждого диапазона находится из опыта и литературных рекомендаций.
Следует заметить, что в учебнике для ВУЗов (Радиопередающие устройства. Под ред. М.В. Благовещенского и Г.М. Уткина, М.: Радио и связь, 1982) добротностью нагруженного контура названа добротность катушки индуктивности П-к на резонансной частоте: ωрL ÷ rL = Q. При этом влияние Xс.вн в ветви с катушкой индуктивности фактически отбрасывалось. Конечно, автор имеет право дать название исследуемому им явлению. Но утверждать при этом, что КПД П-к
Qн
η = 1 - -----,
QXX
где
ωp L ωp L
Qн = --------, QXX = -----
rL + rвн rL
уже некорректно, т.к. ωp холостого хода не равна ωp нагруженного состояния: с изменением Rн меняется Xс.вн, меняется и ωp.
Дано: верхняя частота полосы пропускания fв = 7.2 МГц; Кн(Υmin ) ≥ 0.9; Rэ = Rн = 50 Ом; η ≈ 1.
Находим Qн, которая в таблице согласно заданной неравномерности в полосе пропускания находится в пределах 1.6<Qн<1.8. Применив линейную интерполяцию, находим требуемую Qн = 1.6939.
А можно просто построить по таблице кривую зависимости Кн(Υmin ) от Qн и работать с ней. Тем более, что эта зависимость линейна в диапазоне 1.1<Qн<3, и расчёт можно выполнить по формуле
a - Кн(Υmin )
Qн = -------------- ,
b
,
где a = 1.15612; b = 0.154375. Далее находим величины реактивных сопротивлений,
Xc1р = Xc2р = R÷Qн = 50÷1,6939 = 29,5176; XLр = 43,7778 Ом.
Последнее выражение получено из (11) и (8). Далее требуется найти ωp = 2πf. Можно показать, что для симметричного П-к Υв = ωв÷ωp = 2Υmin. Следовательно,
ωв 2π×7,2×106
ωp = ------ = ---------- = 39,17806×106
2Υmin 1
2×-----
√3
ωp = 39.17806×106 рад ⁄ сек. С1 = С2 = 864.719 пФ; L = 1.11740 мкГн.
Для узкополосного фильтра главное – это фильтрация высокочастотных гармоник. А для сравнительно узкополосных любительских диапазонов ширина полосы пропускания не имеет решающего значения. Могу показать, что коэффициенты передачи напряжения (АЧХ) в согласованном режиме при прямом и обратном включении отличаются лишь постоянным множителем:
R1
KUобр. = KUпр. ---.
R2
В этом можно убедиться и просто расчётами примеров. А теория этого вопроса основана на принципе взаимности из теории линейных электрических цепей.
Чем больше величина QН, тем больше провал в седловине и лучше фильтрация высших гармоник, которая, как показано в [4], улучшается также с увеличением отношения RН ⁄ Rэ.
При увеличенных QН радиолюбители часто отмечают снижение выходной мощности усилителя в высокочастотной области КВ диапазона, особенно в усилителях на лампах с высоким Rэ. Возможно потому, что минимальная входная ёмкость С1 примерно 50 пф. На резонансной частоте
1 RЭ
ХС1р = ----- = ----.
ωp С1 QН
Поэтому при больших значениях RЭ требуется увеличение QН, что может привести к падению КПД П-к и, соответственно, усилителя. В случае применения усилителя на мощных транзисторах его выходное сопротивление достаточно мало, что и снимает эту проблему.
rL
η = 1 - --------- ,
rL + rВН
1
т.е. ----------- = 0.05 или rL < rВН/19.
1 + rВН/rL
RH X2C2P
rВН = ----------- .
R2H + X2C2P
Далее из (9) и (10) находим:
75
XC2P = --------------- = 18.2467 Ом.
75
√-----------(132+1)-1
0.95 * 750
Следовательно, необходимо иметь rL < 0.220588 Ом.
Если катушка индуктивности рассчитана и изготовлена, её добротность QL (это не QН) можно измерить, например, методом последовательного резонанса с учётом того, что добротность конденсатора практически всегда более чем на порядок (10 раз) выше добротности катушки индуктивности. Зная QL, можно вычислить rL = XLр / QL. Измерения надо проводить в реальных условиях работы, с учётом, например, влияния короткозамкнутых катушек соседних диапазонов. Особое внимание при настройке обратить на возможное влияние анодного дросселя на резонансную систему [5].
Далее находим: ХС1р = 750 / 13 = 57.6923 Ом, ХС2р = 18.2467 Ом,
750 0.95 * 75
ХLр = -------- (13 + ----------) = 74.5800 Ом.
132 + 1 18.2467
1 1
С1 = ------- = ----------------------------------- = 129.973 пф
ωp ХС1р 2π*0.5 (21*106+21.450*106)*57.6923
1
С2 = ------- = 410.949 пф
ωp ХС2р
ХLр
L = ----- = 0.559235 мкГн
ωp
Вопросы и свои мнения можно присылать по адресу: E-mail: ra3vfn@yandex.ru Павел Петрович Белоусов
Литература: 1. Г. Шульгин. Методика расчёта П-контура передатчика. – Радио,1985, #5. 2. П. Белоусов. Расчёт П-контура. – Радиомир. КВ и УКВ, 2004, #3. 3. Г. Аглодин. П-контур. – Радиомир. - КВ и УКВ, 2007, #6. 4. П.Белоусов. П-контур в режиме фильтрации.- Радиомир. КВ и УКВ, 2008, №1,№2. 5. П.Белоусов. К вопросу о выборе и расчёте конструкции анодного дросселя. - Радиомир. КВ и УКВ, 2003, №10.